Q2: Random number distributions (8 points)

In this problem, you are going to visualize random number distributions, using a sideways graph of asterisks (which you can 'cout'), eg.:

**********
*********
********
*******
******
*****
*****
******
*******

The code you are going to implement, is for random numbers that fall between 0.0 and 1.0 (not 0 to 32767, etc). Out of N random numbers that you generate (eg. N can be 1000000), you are going to count how many lie between these ranges:

0.0 to 0.1
0.1 - 0.2
0.2 - 0.3
....
0.9 - 1.0

This is called 'binning' (where we assign each random number to one of 10 bins/buckets). If the bins are numbered 0,1,2..9, then you can determine a random number r's bin using:

floor(r*10) // eg. if r is 0.5900345, r*10 is 5.900345, and floor(r*10) is 5 

Once you know what the bin# is, you can keep track of how many numbers fall in a bin, using 10 counters. Given 10 vars a0,a1,a2..a9 all initialized to 0, you can use a set of 'if' statements [or better, a 'switch' statement] to increment the appropriate counter: eg. if a random # falls in bin 5, do 'a5++' to increment that bin's counter.

If you generate N random numbers and do the above binning and track each bin's count, the total bin counts would/should add up to N:

a0+a1+a2+a3...a9 = N

Note: while this is rare, r could be 1.0, in which case, floor(r*10) will be 10 - when this happens, simply increment a9. If you don't do this, you will find that a0+a1..+a9 will be less than N, instead of being equal to it.

Rather than just 'cout' the 10 bin subtotals, you could transform each into a row of *s and cout them instead. Eg. for a5:

nAsterisks = floor(100 * a5/N)
cout a row of nAsterisks *s

So your program would print out 10 rows of *s, one row for each of a0,a1,a2.. a9.

To print nAsterisks *s, you could use a function like so:

void printStars(int n) {
  for(int i=0;i < n;i++) {
    cout << "*";
  }
  cout << endl;
}/// printStars()

...

printStars(nAsterisks) // prints a chain of nAsterisks *s

When all the 10 rows of *s all have nearly equal # of *s, that means the random # distribution is 'uniform' - a random number in such a distribution has equal probability of falling in any of the 10 bins, which is why the bins end up with nearly identical counts (and therefore, *s). This is what your code would show. Here is a sample output:

CourseNana.COM

So, visualize a uniform distribution using asterisks, as described above.

Next, visualize a 'triangular' distribution (eg. see http://en.wikipedia.org/wiki/Triangular_distribution /). To create such a distribution, simply generate two rand() values (each normalized to 0..1) and AVERAGE them together!

r1 = first rand#
r2 = second rand#
r = 0.5*(r1+r2) // values around 0.5 are most likely, endpoints at 0 and 1 are least likely
'bin' r as described above, ie do 'floor(r*10)'

Now your 10 rows of *s will not be all nearly identical, like they were in the uniform distribution case: you should see a peak for 0.4-0.5 and 0.5-0.6, with the * count tapering off on both sides (this makes the distribution look like a triangle). Here is a sample output:

CourseNana.COM

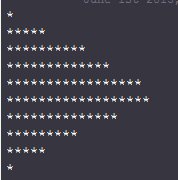
In this modern era of high resolution displays that are in our handhelds even, why bother with visualization using plaintext *s? Because it is much simpler to do so, is a 'portable' solution, and makes for good coding practice :)

seed the rand function with a known seed
double largestVal = -10000000; // a SMALL value
for each of N times
  generate a Pareto value
  if value>largestVal, largestVal=value // we have a new largestVal
next iteration

// now we know the largest value, it's stored in largestVal
RE-seed the rand function with the same seed used earlier (to restart the sequence)
for each of N times
  generate a Pareto value
  divide by largestVal // this will now be 0..1
  'bin' the result

seed the rand function with a known seed
double largestVal = -10000000, smallestVal = 10000000;
for each of N times
  generate a Pareto value
  if value > largestVal, largestVal=value // we have a new largestVal
  if value < smallestVal, smallestVal=value
next iteration

// now we know the largest AND smallest values, use them to normalize 
RE-seed the rand function with the same seed used earlier (to restart the sequence)
for each of N times
  generate a Pareto value 'p'
  pNorm = (p - smallestVal)/(largestVal - smallestVal) // 0..1
  do binning on pNorm